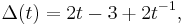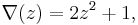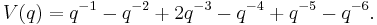Three-twist knot

In knot theory, the three-twist knot is the twist knot with three-half twists. It is listed as the 5₂ knot in the Alexander-Briggs notation, and is one of two knots with crossing number five, the other being the cinquefoil knot.

The three-twist knot is a prime knot, and it is invertible but not amphichiral. Its Alexander polynomial is

$\Delta(t) = 2t-3%2B2t^{-1}, \,$

$\nabla(z) = 2z^2%2B1, \,$

$V(q) = q^{-1} - q^{-2} %2B 2q^{-3} - q^{-4} %2B q^{-5} - q^{-6}. \,$ ^[1]

Because the Alexander polynomial is not monic, the three-twist knot is not fibered.

The three-twist knot is a hyperbolic knot, with its complement having a volume of approximately 2.82812.

References